Tree In Data Structure in Hindi

Computer Science में Data Structure वास्तविक दुनिया में पाए जाने वाले एक Tree ( पेड़ ) की तरह ही होता है, बस अन्तर केवल इतना है कि Computer Science में Tree Data Structure की जड़े (Root) ऊपर होती है और जड़ से ब्रांचेज और Leaves Connect होती है ।

Tree ( ट्री )

Tree एक Non – Linear Data Structure है जो कि Information या Data को Hierarchical (श्रेणीबद्ध) तरीके से Store करता है । वैसे तो tree हमेशा ऊपर की ओर बढ़ता है लेकिन data structure का tree हमेशा नीचे की ओर बढ़ता है।

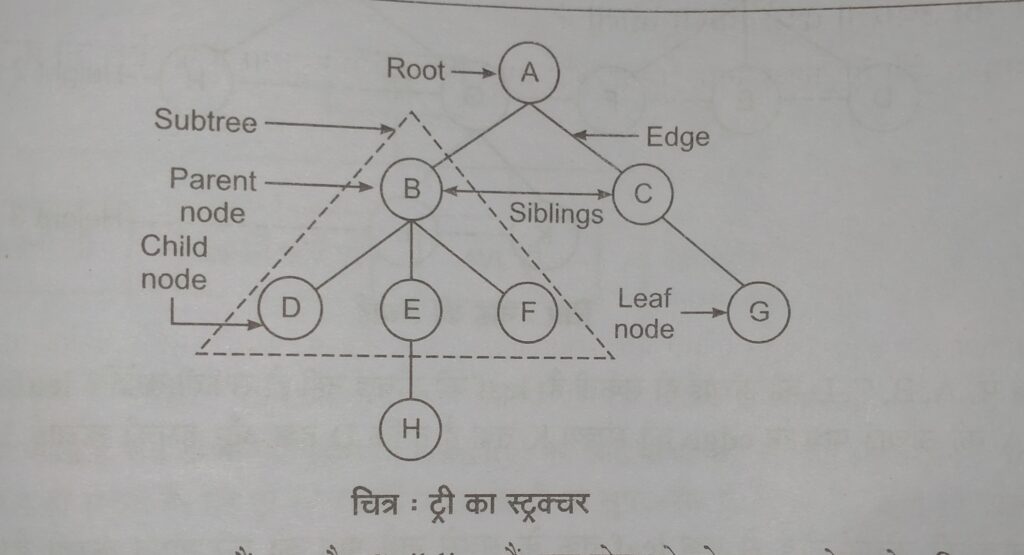
Tree terminology

• Root Node – Root एक ऐसा Node होता है जिसके ऊपर और कोई Node नहीं होता है यानि उसी Node से सारे के सारे Node नीचे की ओर Connect होते है वह हमारा Root Node कहलाता है चित्र में A Node हमारा Root Node है ।
• Parent Node – Parent Node एक ऐसा Node होता है जो किसी Node को Connect करता है। जैसे चित्र में B जो है वह D,E,F का Parent Node है।
• Child Node – वे Node जो किसी से Node से Connect रहते है यानि Parent Node से Connect होते है Child Node कहलाते है जैसे चित्र में, D, E, F जो हैं वे B के Child Node है।
• Siblings – वे Nodes जिनके एक ही Parent होते है उन्हें siblings कहते हैं जैसे चित्र में, B और C siblings हैं.
• Leaf Node – Leaf Node एक ऐसा Node होता है जिसके एक भी Child Node नहीं होते है यानि वह किसी नहीं जुड़ा होता है वह हमारा Leaf Node कहलाता है चित्र में चित्र में, D, H, F, G Leaf Nodes हैं । इन्हे External Node भी कहते है।
• Internal Node – वह Node जिसका कम से कम एक Child Node होता है उसे Internal Node कहते है।
• Edge – एक Edge दो Nodes के मध्य का Connection होता है । यह दो nodes के बीच की line होती है ।
  चित्र में, A और B के बीच की line एक edge है ।
• Digree Of Node -: Node की Digree एक Node के Child Node की संख्या होती है ।

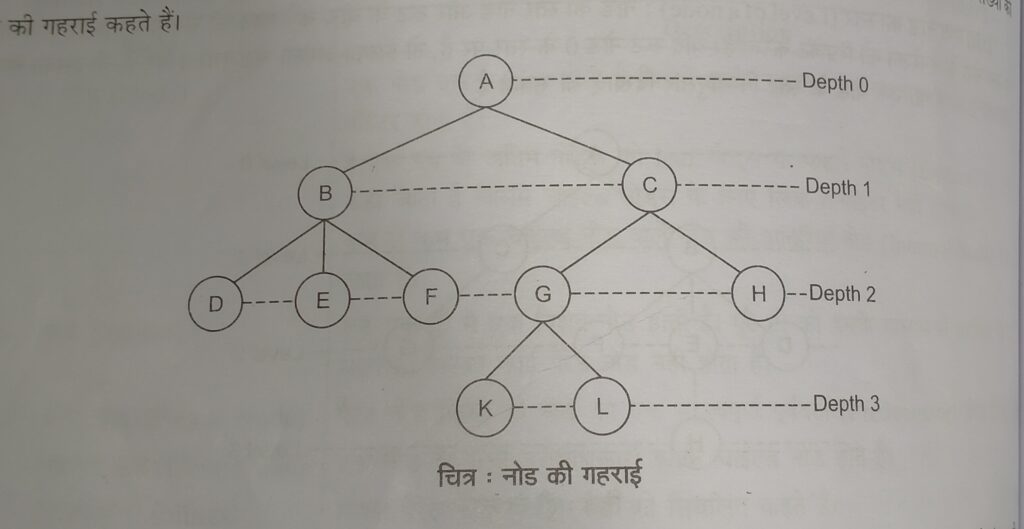
Level Of Node ~ नोड का स्तर

Node का Level,Node और Root के बीच Connection की संख्या को प्रदर्शित करता है । और यह एक Node के Generation के भी Represent करता है ।

यदि Root Node (शुन्य ) 0 Level पर है, तो इसका अगला Node Level 1 पर है, तो इसका Child Node Level 2 पर होगा । एक Node के Level निम्नानुसार दिखाए जा सकते है।

Height of a node ~ एक नोड की ऊंचाई

एक Node की ऊंचाई Node और एक Leaf के बीच सबसे लम्बे पाथ यानि जो लम्बी श्रृंखला होगी उस पर Edge की संख्या को Represent करती है।

Depth of a node ~ एक नोड की गहराई

किसी Node की गहराई, Tree के Root Node से उस Node तक पहुचने वाले पाथ की लम्बाई होती है।

Types Of Tree ~ ट्री के प्रकार

Tree के निम्नलिखित प्रकार होते है –

• General Tree
• Binary Tree
• Binary Search Tree
• AVL Tree
• Red – Black Tree
• N – Ary Tree

1. General Tree

General Tree एक ऐसा Tree होता है जिसमें एक Node के कितने भी Child Node हो सकते है इसमें Child Node पर कोई रोक नहीं होती है। इसमें एक Node के पास Zero ( शून्य ) Child Node हो सकते है या फिर बहुत सारे Child Node हो सकते है।

2. Binary Tree

Binary का मतलब होता है दो 0 और 1, तो Binary Tree एक ऐसा Tree होता है जिसमें प्रत्येक Node के पास अधिकतम दो child Nodes ही हो सकते है। ऐसे Tree को Binary Tree कहते है।

3. Binary Search Tree

Binary Search Tree इसे BST भी कहते है यह एक Binary Tree ही होता है Binary Search Tree में Node के Left Child या Left Node की Value उसके Parents Node की Value से कम या उसके बराबर होनी चाहिए और Right Child Node या Right Node की Value हमेशा Parent Node के Value से अधिक या बराबर होनी चाहिए और इसमें कोई भी Node Dublicate नहीं होना चाहिए ।

4. AVL Tree

• AVL Tree एक Self Balancing Binary Search Tree है ।
• AVL नाम इसके अविष्कारकों एडलसन – वेल्शी और लैंडिस के नाम पर दिया गया है ।
• AVL TREE को Height Balanced Tree भी कहा जाता है। इसके पास एक extra जानकारी होती है जिसे Balance factor कहते हैं ।
• AVL TREE का प्रयोग डेटा को organise करने के लिए किया जाता है।

5. Red – Black Tree

Red – Black Tree भी एक Self Balancing Binary Tree है इसे Red – Black नाम इसलिए दिया गया है क्योंकि Red – Black Tree में प्रत्येक Node को Red – Black Tree की Properties के अनुसार या तो Red या Black Print कर दिया जाता है।

6. N – Ary Tree

इसमें एक N – Ary Tree में, एक Node में Child Node की अधिकतम संख्या N तक सीमित हो सकती है । एक Binary Tree 2 – Ary Tree है, क्योंकि Binary Tree में प्रत्येक Node की अधिकतम 2 Child Node ही होते है।

Advantage Of Tree ~ ट्री के लाभ

• Tree का सबसे बड़ा फायदा यह है कि इसके द्वारा हम Data को Hierarchical (श्रेणीबद्ध) तरीके से स्टोर कर सकते हैं ।
• इसके द्वारा हम आसानी से searching और traversing कर सकते हैं ।
• Tree बहुत ही flexible होता है अर्थात् इसमें हम किसी भी sub-tree को आसानी से move कर सकते हैं ।
• इसके द्वारा हम data को तेजी से search, insert और delete कर सकते है ।

Application Of Tree ~ ट्री के अनुप्रयोग

1. Tree एक Non – Linear Data Structure है इसलिए इसका प्रयोग Data को Hierarchical तरीके से store करने के लिए किया जाता है ।
2. इसका प्रयोग Data को कुशल रूप से Organize (व्यवस्थित) करने के लिए किया जाता है ।
3. Binary Search Tree का प्रयोग तेजी से Data को Search, Insert, Delete करने के लिए किया जाता है ।
4. Heap एक Tree है जिसका प्रयोग Priority Queue को Implement करने के लिए किया जाता है ।
5. Binary Tree का प्रयोग Database में Indexing को Implement करने के लिए किया जाता है ।
6. इसका प्रयोग Artificial Intelligence में किया जाता है ।
7. Games को बनाने में इसका इस्तेमाल किया जाता है।